Six points are scattered around space so that no three are collinar and no four are co-planar. The points are named 1, 2, 3, 4, 5, and 6. Each point is connected every other point by a tubular neon light that is either red or blue. Show that there is a neon tubular light triangle that is a single color: red or blue.
Solution
This problem is the same as 3060.61. The restrictions on the spacial arrangement of the points is simply to ensure that the neon tubes do not cross. Here is the solution of 3060.61, adapted for this situation.
In the figure below, points are connected by lines that signify either red tubes (dashed lines) or blue tubes (solid lines). There are two classes of point: points with more red than blue tubes, that is, having at least three red tubes. Call these points points. There are also (possibly) points with more blue than red tubes. Call these points points.
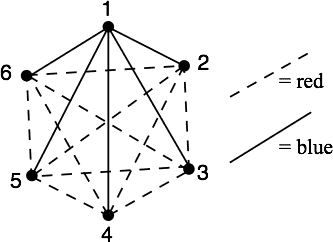
Pick one point, say 1 which happens to be a point. That means 1 is connected by a blue tube with three other points. Now if at least one pair among the points with which 1 has a blue connection are connected by a blue tube, then right there there is a blue triangle (including 1). And if none of the 3 points to which 1 is connected by a blue tube shares has a blue tube connection (as is the case in the figure), then there is a red triangle. That proves what we want, if 1 happens to be a point.
You can complete the argument in case 1 happens to be a point.