3060.61 – People In Groups

Six people form a club. In the club, two people either like each other or dislike each other. Show that either there is a group of three all of whom like each other OR there is a group of three all of whom dislike each other.

Solution

For convenience put the six people around a circle as in the figure below. Connect people who like each other. There are two classes of person:

People that like more than they dislike, that is, they like at least three others. Call these people class $\mathcal{L}$ .
People who dislike more than they like. Call these people class $\mathcal{D}$ .

Pick one person, $A$ , who is in class $\mathcal{L}$ . This means $A$ likes at least three others. Say that these are $B$ , $C$ , and $D$ , as in the figure.

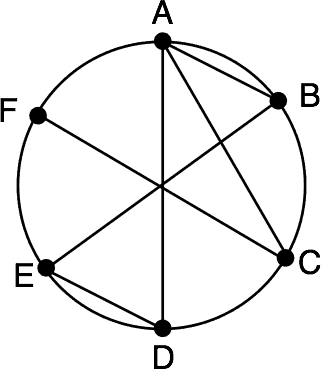
Now if at least one other pair among $B$ , $C$ , $D$ like each other then right there there is a group (including $A$ ) of three people who mutually like each other. Otherwise, if none of $B$ , $C$ , and $D$ like each other (as is the case in the figure), then there is a group of three people who dislike each other. That proves what we want, if $A$ happens to be in class $\mathcal{L}$ .

Complete the argument in case $A$ happens to be in class $\mathcal{D}$ .