3060.53 – Red and Blue Point Parallelogram

Suppose that every point in a plane is colored either red or blue. Show that there is a parallelogram somewhere in the plane whose vertices are all the same color.

Solution

To start, there is at least a red triangle $\triangle ABC$ . (See 3060.52 for a proof of this.) The rest of the discussion refers to the diagram below.

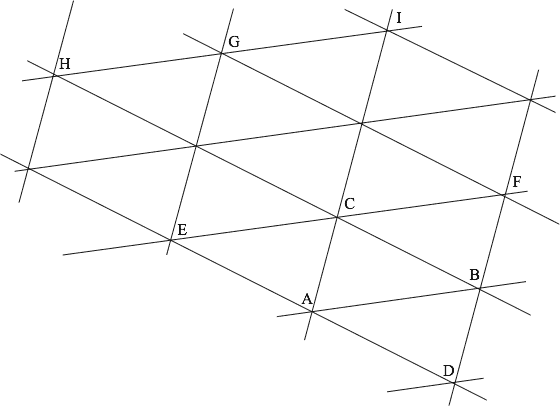
If any of $D$ , $E$ , or $F$ are red then there is a red parallelogram: $\square ACBD$ for example. Therefore, assume all three points are blue.

If $G$ is blue, then $\square DEGF$ is blue. So assume $G$ is red.

If $H$ is red, then $\square ABGH$ is red. So assume $H$ is blue.

Finally consider $I$ . If $I$ is blue, then $\square FEHI$ is blue while if $I$ is red, $\square ABIG$ is red. That's it!