3060.52 – Red and Blue Point Triangle

Suppose every point in a plane is colored either red or blue. Show that there is an triangle somewhere in the plane whose vertices are all the same color.

Solution

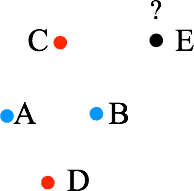
Find two points, $A$ and $B$ , that are the same color, say blue. Then make a triangular array of points as shown in the figure above.
If $C$ or $D$ is blue, we're done. So assume $C$ is red, and $D$ is red.
If $E$ is red, we're done, $\triangle CDE$ is red. If $E$ is blue, then we're done, $\triangle ABE$ is blue.