The flight from New York to Honolulu takes 11.5 hours. Halfway there, having seen two movies, your phone dies. What are you going to do? You can't sleep for the next 6 hours! Just then the pilot announces that the plane has changed altitude. You are now at a height of 10 km. Looking out the window at a clear sky you see the horizon.
Given that the radius of the earth is approximately 6400 km, just how far away is the horizon? Think of the horizon as a spot, and then (second task) tell how far that spot is from the spot just beneath the plane, if you were sailing from one to the other, taking the curvature of the earth into account.
Solution
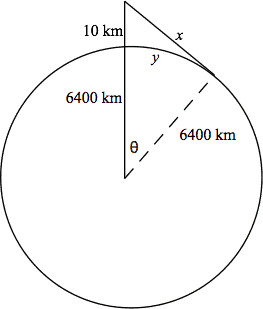
Referring to the diagram above (not drawn to scale), we first calculate the distance – this is how far away that point is from you. This requires only the Pythagorean theorem. Note that the distance of the plane from the center of the earth is 6410 km.
To find the distance along the earth's surface, we first find the angle and then .
The two distances are about the same, of course.