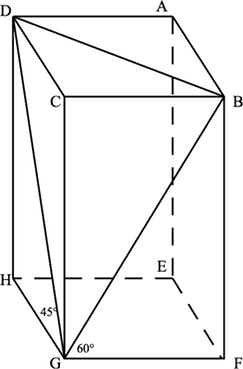
4200.11 – Tetrahedron Cutoffs

Here is a rectangular solid with ∠DGH=45∘\angle DGH = 45^\circ and ∠FGB=60∘\angle FGB = 60^\circ. What is cos⁡(∠BGD)\cos(\angle BGD)?

Solution

Assume, for convenience, that GH=1GH = 1. Then DH=1DH = 1 and DG=2DG = \sqrt{2}. Also, DC=1DC = 1, BC=33BC = \dfrac{\sqrt{3}}{3} because CG=1CG = 1 and DB=233DB = \dfrac{2\sqrt{3}}{3}.

Now, △BDG\triangle BDG is iscosceles, so when we draw BMBM to the midpoint of DGDG, we have a right angle at MM.

So △BMG\triangle BMG is a right triangle and now we can nail down the desired cosine.

cos⁡(∠BGD)=2/223/3=22⋅322=32⋅343⋅3=3612=64\begin{aligned}\cos(\angle BGD) &= \dfrac{\sqrt{2}/2}{2 \sqrt{3}/3} \\[1em]&= \dfrac{\sqrt{2}}{2} \cdot \dfrac{3}{2 \sqrt{2}} \\[1em]&= \dfrac{3 \sqrt{2} \cdot \sqrt{3}}{4 \sqrt{3} \cdot \sqrt{3}} \\[1em]&= \dfrac{3 \sqrt{6}}{12} = \dfrac{\sqrt{6}}{4}\end{aligned}