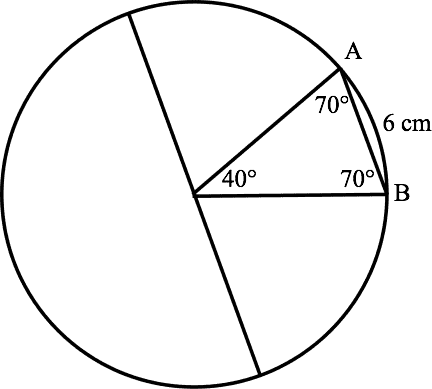
In a given circle a central angle of 40 degrees intercepts a chord of 6 cm. What is the circumference of the circle?
Solution
\angle B = \angle A = 70 degrees.
By the law of sines, the radius is x/sin 70 degrees = 6/sin 40 degrees \rightarrow x = 6(sin 70 degrees/sin 40 degrees).
The circumference is 2 x, or 2 * 6(sin 70/sin 40) \approx 12 (3.14)(.94)/.64 \approx 55.34 cm
(Note: The diameter of the circle is about 55.34/3.14, or 17.6. The radius is about 8.8, not a whole lot more than that chord.)
