The pair of figures below suggests that . What is wrong?
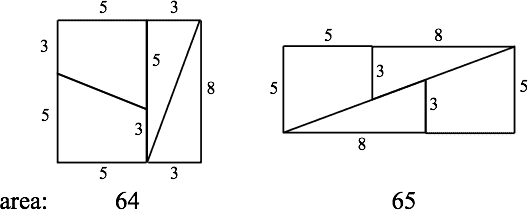
The supposed paradox in this problem uses the particular numbers 3, 5 and 8, Actually the paradox can be replicated using any three consecutive numbers in the sequence: where each number is the sum of the previous two. This sequence is called the Fibonacci sequence, hence the name of this problem.
The paradox, incidentally, looks better and better, i.e., more and more mysterious, the further out in the sequence the numbers are taken.
Solution
If you draw the second figure carefully and at a larger scale, as is done below, the missing area shows up as a tiny parallelogram of area 1.
