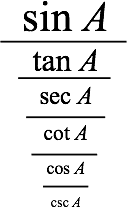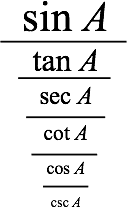4100.11 – Compound Fraction: Trig

Simplify this compound fraction:

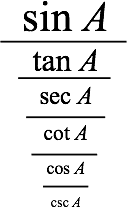
4100_11_5e332f945a.png

Solution

We start at the bottom.

cosAcscA=cosA1sinA=cosA⋅sinA\frac{cos A}{csc A} = \frac{cos A}{\frac{1}{sin A}} = cos A \cdot sin A.

cotAcosA⋅sinA=cosAsinA⋅1cosA⋅sinA=1sin2A\frac{cot A}{cosA \cdot sinA}=\frac{cos A}{sin A} \cdot \frac{1}{cos A \cdot sin A} = \frac{1}{{sin^2}A}.

secA1sin2A\frac{sec A}{\frac{1}{sin^2 A}} = secA⋅sin2Asec A \cdot{sin^2 A} = 1cosA⋅sin2A\frac{1}{cos A} \cdot {sin^2} A = sin2AcosA\frac{{sin^2} A} {cos A}.

tanAsin2AcosA\frac{tan A}{\frac{{sin^2} A} {cos A}} = sinAcosA⋅cosAsin2A\frac{sin A}{cos A} \cdot \frac{cos A}{{sin^2} A} = 1sinA\frac{1}{sin A}.

sinA1sinA=sin2A\frac{sin A}{\frac{1}{sin A}} = {sin^2 A}.

After all that!