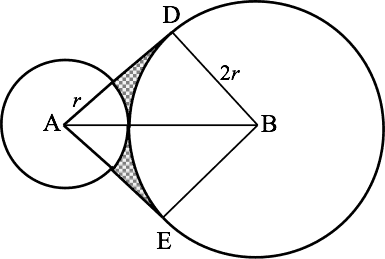
4050.12 – Area External to Two Circles

A circle of radius rr is externally tangent to a circle of radius 2r2r, as in the figure. Segments ADAD and AEAE are drawn tangent to the circle with center at BB. Find the area of the shaded region.

Solution

Let A\mathcal{A} be the shaded area. Then

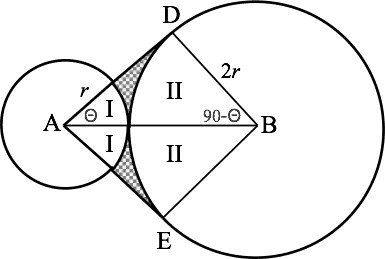
A=2(ΔADB−I−II)\mathcal{A} = 2(\Delta ADB - \text{I} - \text{II})

For the area of ΔADB\Delta ADB, we need the length ADAD:

AD=(3r)2−(2r)2=r5AD = \sqrt{(3r)^2 - (2r)^2} = r\sqrt{5}

ΔADB=r5⋅(2r)2=r25\Delta ADB = \dfrac{r\sqrt{5} \cdot (2r)}{2} = r^2\sqrt{5}

For the area of sectors I\text{I} and II\text{II} we need the angle Θ\Theta:

Θ=arcsin⁡(2r3r)=arcsin⁡(23)\Theta = \arcsin\left(\dfrac{2r}{3r}\right) = \arcsin\left(\dfrac{2}{3}\right)

I=Θ360πr2, II=90−Θ360π(2r)2I = \dfrac{\Theta}{360} \pi r^2, \ II = \dfrac{90-\Theta}{360} \pi (2r)^2

Putting this all together:

A=r2(25+π(arcsin⁡(23)360+90−arcsin⁡(23)90))\mathcal{A} = r^2 \left( 2 \sqrt{5} + \pi \left(\dfrac{\arcsin{\left(\dfrac{2}{3}\right)}}{360} + \dfrac{90 - \arcsin{\left(\dfrac{2}{3}\right)}}{90}\right) \right)