An equilateral triangle with side length 2 is inside a square with side length 4, as shown in the figure. The triangle rolls along the inside of the square, first rotating clockwise about L and then around the corner where A lands. And so on. The triangle rolls along the sides of the square until all three vertices return to their original positions.
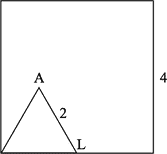
Which of these gives the length of the path traversed by vertex A?
(a) 20 /3, (b) 32/3, (c) 12, (d) 40/3, (e) 15.
Solution
Our point A makes a lengthy and complicated journey.
This is a problem where it helps if you get your hands dirty and either actually move a triangle around on a table or at least imagine that is happening. The figure below may help.
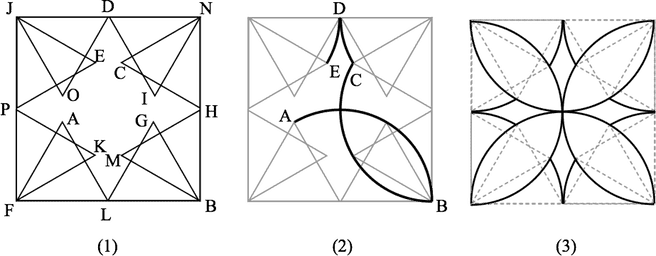
Part (1) of the figure shows all the positions of the triangle as it rolls around the inside of the square. The labels on the vertexes A, B, and so on are (in alphabetical order) the points where the vertex A stops on its journey.
Part (2) of the figure shows the path traced by A for its first four stops: A-B-C-D-E. In order for A to get to E the triangle actually rotates 6 times. For two of these rotations, A doesn't move because it is the center of the rotation. That's why it takes 6 rotations for A to make 4 stops.
Part (3) of the figure shows the whole path followed by A. Note that some parts of the path are traced out twice.
What about the length of the path? If you think about the point A along these lines, you will realize that as the triangle rotates, A makes three kinds of moves. Some moves are long ones: 120° around a circle of radius 2. The length of one of these long moves is
There are also short moves, also around a circle of radius 2. These are 30° of the circle and have length
Finally, when A lands on corners or edges, it pauses briefly and traces out zero in length.
There are 8 long moves, 8 short moves, and 8 zero moves. The total trip is . The answer is (d).
