3695.11 – A Square in a Cube

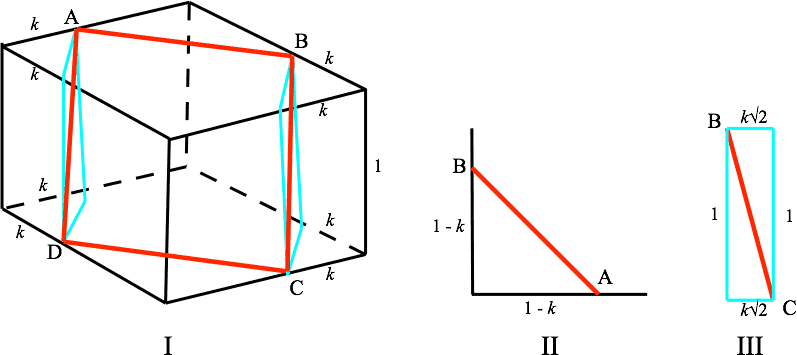
The figure shows a cube with unit edge and four points A,B,C,DA, B, C, D, placed on four edges at a distance kk from a vertex, where 0≤k≤10 \le k \le 1.

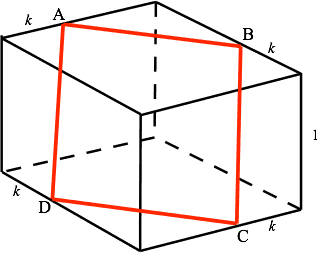
  1. The quadrilateral ABCDABCD is planar. Justify this assertion.

  2. Find all values of kk that make ABCDABCD a square.

  3. What are the sides of those squares?

Solution

  1. For students who are comfortable in 3-dimensional analytic space, it is easily checked that the equation of the plane containing ABCD is x−y+2kz=kx - y + 2 k z = k. For others, we are groping for a good old-fashioned Euclidean justification. The old "as any fool can plainly see" is tempting. If any of you out there can help with this, please do so!

  2. ABCDABCD is a square when AB=BCAB = BC. We express both those lengths in terms of kk, set them equal and solve.

    For ABAB we see from the figure, part I, that it is the hypotenuse of an isosceles right triangle with legs of length 1−k1 - k. That makes AB=(1−k)2AB = (1 - k) \sqrt{2}. See the figure, part II.

    As for BCBC, it is the diagonal of a rectangle with sides of length k2k \sqrt{2} and 11. This makes BC=2k2+1BC = \sqrt{2 k^2 + 1}.

    Setting these two equal, we find that

    AB2=BC2,2(1−k)2=2k2+1,2k2−4k+2=2k2+1,−4k=−1.\begin{aligned}AB^2 &= BC^2, \\2 (1 - k)^2 &= 2 k^2 + 1, \\2 k^2 - 4 k + 2 &= 2 k^2 + 1,\\-4 k &= -1.\end{aligned}

    The only value of kk that works is 1/4.

  3. For k=1/4k = 1/4, the side is

    AB=(1−k)2=324.AB = (1 - k) \sqrt{2} = \dfrac{3 \sqrt{2}}{4}.

    Check:

    BC=2k2+1=2116+1=98=322=324\begin{aligned}BC &= \sqrt{2 k^2 + 1} \\&= \sqrt{2 \dfrac{1}{16} + 1} \\&= \sqrt{\dfrac{9}{8}} \\&= \dfrac{3}{2 \sqrt{2}} \\&= \dfrac{3 \sqrt{2}}{4}\end{aligned}