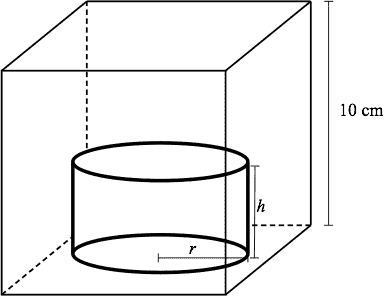
Water pours at a constant rate into a one-liter cube, which therefore is cm on each side. The water level rises to the halfway mark, then continues to rise at exactly half the previous rate. That's because inside the cube is a cylindrical can attached to the bottom as in the figure.
What are the height and radius of the can?
Solution
Let be the height and be the radius of the can. What happens is that the water rises until it reaches the top of the can. Since the water level changes its rate of rising halfway up the cube, it must be that . Since the water continues to rise but at half the previous rate, the crossection of the can is a circle whose area is exactly half the area of a crossection of the cube. In other words,
so that .