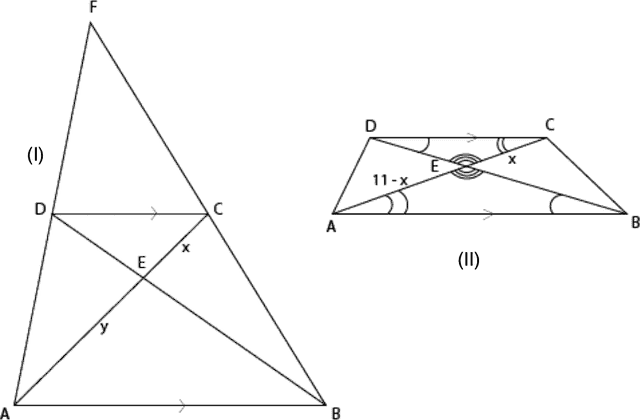
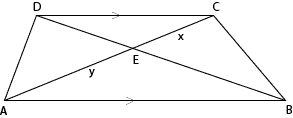
Let be a trapezoid with the length of base twice that of base , and let be the point of intersection of the diagonals. If the length of diagonal is 11, what is the length of segment ? The picture below is not to scale.
Solution
Referring to the figure, part (I), we know ; we want which we call . Extend and to meet at , forming . Because and , we know and . Also, . Thus and are medians, intersecting each other in the ratio . So , , , and
The answer is (a).
Alternatively, consider triangles and as in the figure, part (II). Since and are parallel, , and . Lines and intersect at point , so .
Since the angles of the two triangles are the same measure, we can say , which means that . We note that and , so that to rewrite the equation as . Solving for , we get, again, that .
The answer, once again, is (a).