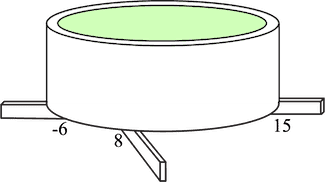
3520.11 – The Balancing Pot

Here is a pot, balanced on a pair of steel slabs that meet at right angles below the pot. The intersection of the slabs is treated here as the origin of a set of co-ordinate axes which hit the edge of the pot at the distances −6-6, 1515, and 88 as shown.

What is the diameter of the pot?

Solution

The problem gives, in effect. three points on a circle as in the figure below. As three points determine a circle, it should be possible to find the equation of this one:

(x−h)2+(y−k)2=r2, (x-h)^2 + (y-k)^2 = r^2,

where (h,k)(h, k) is the location of the center, and so determine the radius rr. Plugging in the three points gives the three equations:

36+12h+h2+k2=r2,225−30h+h2+k2=r2,h2+64−16k+k2=r2.\begin{aligned}36 + 12 h + h^2 + k^2 &= r^2, \\225 - 30 h + h^2 + k^2 &= r^2, \\h^2 + 64 - 16 k + k^2 &= r^2.\end{aligned}

Subtracting the equations in pairs gives

42h−189=0,36+12h−64−16k=0.\begin{aligned}42 h - 189 &= 0, \\36 + 12 h - 64 - 16k &= 0.\end{aligned}

These two linear equations are easily solved. It turns out that h=189/42=9/2h = 189/42 = 9/2 and k=−26/16=−13/8k = -26/16 = -13/8. Plugging this information into any of the first three equations, we discover that r=85/4=21.25.r = 85/4 = 21.25.