3500.31 – Circle Around Three Squares

Each side of each square in the figure below has length 1 unit. What's the radius of the smallest circle containing the symmetric figure composed of the three squares as shown?

a. $\sqrt{2}$

b. $\sqrt{1.25}$

c. 1.25

d. 5 $\sqrt{17}$ /16

e. none of these

Solution

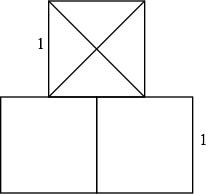
Consult the figure below.

We'll design a circle passing through A, B, C, and D. Its center O will be on the line EF bisecting the symmetry line of the figure. Its its radius will be $x$ .

Note that $x$ is the hypotenuse of two right triangles, OEB and OFD. Let OF = $t$ . Then OE = $1 + (1 - t) = 2 - t$ . Now $x^2 = t^2 + 1^2$ and $x^2 = (2 – t)^2 + (1/2)^2$

Here we go:

\begin{aligned} t^2 + 1 &=& 4 - 4t + t^2 + ¼, \\ 4t &=& 3 + \frac{1}{4}, \\ t &=& \frac{13}{16}. \end{aligned}

So, in \triangle OFD,

\begin{aligned} x^2 &=& (\frac{13}{16})^2 + 1^2 \\ &=& \frac{169}{256} + \frac{256}{256} \\ &=& \frac{425}{256}= \frac{25\cdot17}{256},\\ x &=& \frac{5\sqrt 17}{16}. \end{aligned}

We see that $x$ is approximately 1.29, not so very different from answer choice (c), but (d) is exact. Were you to draw the figure with sides of one inch and make a careful measurement you'd get just about an inch and a quarter for the radius.