3500.21 – Midpoint of a Chord?

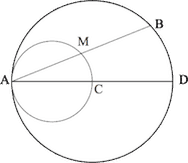
The radius of the large circle is twice the radius of the small one. The circles are internally tangent at $A$ . $B$ is any point on the large circle. $AB$ intersects the small circle at $M$ . Is $M$ the midpoint of $AB$ ?

Solution

Draw diameter $AD$ , which passes through $C$ , the center of the large circle. Draw $MC$ and $BD$ . $\triangle AMC$ and $\triangle ABD$ are right triangles that are similar because they have congruent angles. Thus, since $AD = 2AC$ , we have $AB = 2AM$ , so $M$ is indeed the midpoint of $AB$ .