3475.11 – The Unknown Edge

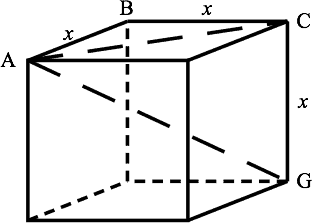
Let $x$ be the unknown edge length. In the figure, the diagonal of the cube, which we are given is 20, is $AG$. It is also the hypotenuse of $\triangle ACG$. By the Pythagorean Theorem, using that $AC = x\sqrt{2}$,

$20 = AG = \sqrt{(x\sqrt{2})^2 + x^2} = \sqrt{3x^2}.$

Solving for $x$,

This is the Pythagorean Theorem in three dimensions:

$AG^2 = x^2 + x^2 + x^2.$

It works for a rectangular solid (not just a cube) and actually works in any number of dimensions as well!