3470.32 – Cardboard Box

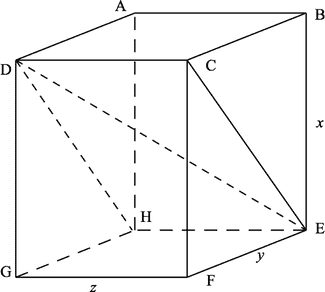
You have a cardboard packing box whose internal dimensions are 24 inches by 18 inches by 16 inches. You have several long objects to pack away for the summer – a conductor's baton, a bagpipe changer, and so forth. What is the longest object that will fit in the box, assuming that nothing else will get in its way?

Solution

Referring to the diagram, we want the length of $DE$ , the diagonal of the box. It's the hypotenuse of triangle $DCE$ .

Let $DC = z$ . Now $CE$ is the hypotenuse of triangle $CFE$ , so $CE = \sqrt{x^2 + y^2}$ .

Continuing, $DE^2 = DC^2 + CE^2$ , so $DE = \sqrt{z^2 + (\sqrt{x^2 + y^2})^2}=\sqrt{x^2+y^2+z^2}$ .

For our box, the longest object that will fit is $\sqrt{24^2+18^2+16^2}=34$ inches.

NOTE: This is the 3-dimensional version of the Pythagorean Theorem.