3470.14 – Square with Internal Segments

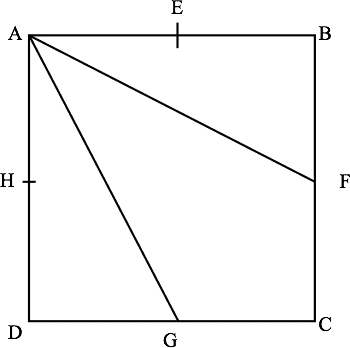
Consider a square with sides each having length 2. Segments are drawn from one vertex to the midpoints of each of the four sides of the square. What is the sum of the lengths of these segments?

Solution

We want $AE + AF + AG + AH$. Well, $AE + AH = 2$.

$AF = \sqrt{2^2 + 1^2} = \sqrt 5$, so $AF + AG = 2\sqrt 5$.

So our total is $2 + 2\sqrt 5$.