3460.11 – Split That Triangle!

A vertical line divides the triangle with vertices $(0,0), (1,1)$ and $(9,1)$ in the $xy$ -plane into two regions of equal area. What is the equation of the line?

$x = 2.5$
$x = 3.0$
$x = 3.5$
$x = 4.0$
$x = 4.5$

Solution

Please refer to the diagram below.

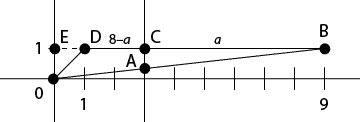
The area of $\Delta\mathsf{OBD}$ is split in half by line $\mathsf{CA}$ . Since $\Delta\mathsf{OBD}$ has base $\mathsf{BD} = 8$ and altitude $\mathsf{EO} = 1$ , its area is

$\mathcal{A}(\triangle \mathsf{OBD}) = (8 \times 1)/2 = 4.$

This means

$\mathcal{A}(\triangle \mathsf{ABC}) = 2 = a(\mathsf{CA})/2.$

Now $\mathsf{CA} \parallel \mathsf{OE}$ , so triangles $\Delta\mathsf{BAC}$ and $\Delta\mathsf{BOE}$ are similar and $\mathsf{CA/OE = BC/BE}$ , i.e., $\mathsf{CA/1 = a/9}$ . Now,

$\mathcal{A}(\triangle \mathsf{ABC}) = a(CA)/2 = a^2/18.$

But this area is also 2. Therefore, $a^2/18 = 2$ and so $a = 6$ .

Thus line $\mathsf{CA}$ intersects the $x$ -axis at $x=3$ , and that's the equation of line $\mathsf{CA}$ : $x = 3$ .

The answer is (b).

What a good problem!