3440.41 – First: Trisect the Diameter

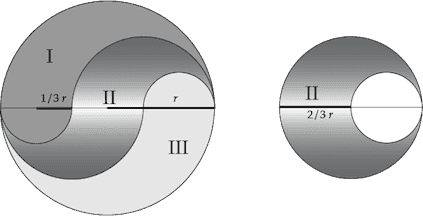
There are several ways to trisect a circular region, but this is one of the prettiest. Trisect the diameter, and then draw semicircles on it as shown. Your job is to prove that the three wavy regions have the same area. You may assume that the area of I equals the area of III.

3440_41_f28a17b541.png

Solution

We already know that the area of region I is equal to the area for region III. We just have to show that the area of region II equals the area of region I. So, we take a breath and find the area of the two regions and show that they are the same. (We will be showing this for some radius r, but this is just as easy to show with your favorite number.) To that end,

AI=πr22–π(r/3)22–π(2r/3)22=πr22+πr218–2ππr29=πr23A_I = \frac{\pi r^2}{2} – \pi \frac{(r/3)^2}{2} – \pi \frac{(2r/3)^2}{2} = \frac{\pi r^2}{2} + \frac{\pi r^2}{18} – \frac{2\pi \pi r^2}{9} = \frac{\pi r^2}{3}

Then, as indicated on the right in the figure, area II is just a circle of radius 2r/3 with a circle of radius r/3 cut out of it. So:

AII=π(2r3)2–π(r3)2=πr2(49–19)=πr23=AI=AIIIA_{II} = \pi (\frac{2r}{3})^2 – \pi (\frac{r}{3})^2 = \pi r^2(\frac{4}{9} – \frac{1}{9}) = \pi \frac{r^2}{3} = A_I = A_{III}

3440_41_solution_2c2f7bec4c.png