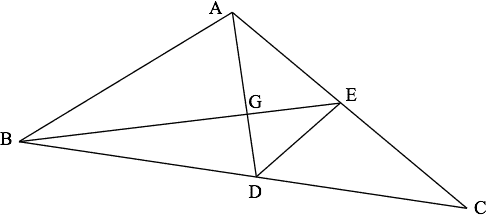
3420.81 – Intersecting Medians

In $\triangle ABC$ , medians $AD$ and $BE$ intersect at $G$ and $ED$ is drawn. If the area of $\triangle EGD$ is $k$ , find the area of $\triangle ABC$ .

Solution

Look at $\triangle BED$ . Medians intersect in the ratio $2:1$ , so set $BG = 2x$ and $GE = x$ . Thus the area of $\triangle BGD$ is $2 \times \text{Area}(\triangle EGD) = 2k$ .

Then look at $\triangle BEC$ . $\text{Area}(\triangle BED) = \text{Area}(\triangle CED)$ , since their bases and heights are respectively equal in length. $\text{Area}(\triangle BED) = 3k$ so $\text{Area}(\triangle CED) = 3k$ too.

Now consider $\triangle ADC$ . $\text{Area}(\triangle AED) = \text{Area}(\triangle CED)$ using the same argument used above, so $\text{Area}(\triangle AEG) = 2k$ .

Finally look at $\triangle BAC$ . $\text{Area}(\triangle BAE) = \text{Area}(\triangle BCE) = 6k$ , so $\text{Area}(\triangle BAG) = 4k$ .

So we've got $12k$ total.

(There might be snazzier ways to get it.)