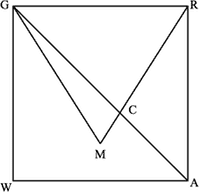
If is a square, and the triangle is equilateral, what is the area of triangle ?
Solution
If the side of the square is and is the height of the , then the area of .
Now, and , so and . This leads to
And now, how about the area of ?

If is a square, and the triangle is equilateral, what is the area of triangle ?

If the side of the square is and is the height of the , then the area of .
Now, and , so and . This leads to
And now, how about the area of ?
