3420.43 – Regular Triangle, Regular Hexagon

An equilateral triangle and a regular hexagon have the same perimeter. If the triangle's area is 2 square units, what is the area of the hexagon? (Hint: Partition.)

Solution

Suppose the triangle's perimeter is 12. Then each of its sides is 4, and each side of the hexagon is 2.

Partition the two shapes into congruent equilateral triangles. There are four in the original triangle and six in the hexagon.

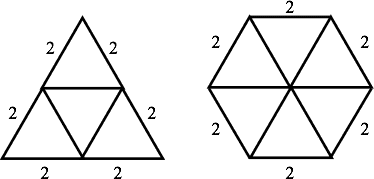
Since the original triangle's area is 2, each small one has area $\dfrac{1}{2}$ .

So the hexagon's area is 6 x $\dfrac{1}{2} = 3$ . Nice problem, eh?