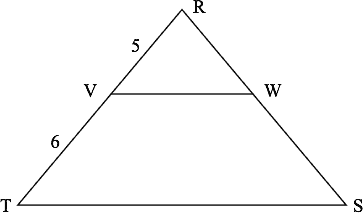
Find the ratio of the area of the triangle to the area of the trapezoid , where is parallel to .
Solution
The triangles and are similar, therefore the bases are in the ratio . The bases themselves will be, say, and respectively, where is a constant.
The heights of the two triangles are in the same ratio, say, and . Therefore the ratio of the areas ( of the triangles is
Now if the area of is , then the area of the trapezoid is and the ratio of these areas is,