3420.27 – Triangle Area

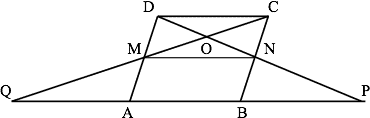
In parallelogram ABCDABCD, MM and NN are midpoints of sides ADAD and BCBC, respectively. CMCM and DNDN intersect at point OO. DNDN intersects ABAB at PP, and CMCM intersects ABAB at QQ. If the area of parallelogram ABCDABCD is 24 cm224 \ \cm^2, find the area of triangle △QPO\triangle QPO.

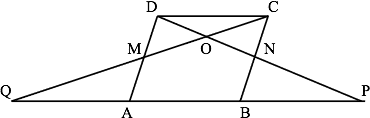
Solution

Master plan:

△QPO=□ABNM+△MNO+△QAM+△BPN.\triangle QPO = \square ABNM + \triangle MNO + \triangle QAM + \triangle BPN.

Here goes:

ABNM=12ABCD△MNO=12△MNC, (half the base MC, same altitude)=12(12MNCD)=12(12(12ABCD))=18ABCD,△QAM=△CDM=12(MNCD)=12(12ABCD)=14ABCD.\begin{aligned}ABNM &= \dfrac{1}{2} ABCD \\[1em]\triangle MNO &= \dfrac{1}{2}\triangle MNC, \text{ (half the base MC, same altitude)} \\[1em]&= \dfrac{1}{2}\left(\dfrac{1}{2}MNCD\right) = \dfrac{1}{2}\left(\dfrac{1}{2}\left(\dfrac{1}{2}ABCD\right)\right) = \dfrac{1}{8}ABCD, \\[1em]\triangle QAM &= \triangle CDM = \dfrac{1}{2}(MNCD) = \dfrac{1}{2}\left(\dfrac{1}{2}ABCD \right) = \dfrac{1}{4} ABCD.\end{aligned}

Likewise, △PBN=14ABCD\triangle PBN = \dfrac{1}{4} ABCD. So (see the top)

△QPO=12ABCD+18ABCD+14ABCD+14ABCD=98ABCD=98⋅24=27 sq cm.\begin{aligned}\triangle QPO &= \dfrac{1}{2} ABCD + \dfrac{1}{8} ABCD + \dfrac{1}{4} ABCD +\dfrac{1}{4} ABCD \\[1em]&= \dfrac{9}{8}ABCD = \dfrac{9}{8} \cdot 24 = 27 \text{ sq cm}.\end{aligned}