3360.11 – Mystery Trapezoid

In the figure, ABAB is parallel to CDCD, and the measure of ∠D\angle D is twice that of angle BB. What is ABAB in terms of aa and bb?

  1. ab+2b\dfrac{a}{b} + 2b

  2. 3b2+3a4\dfrac{3b}{2} + \dfrac{3a}{4}

  3. 2a−b2a - b

  4. 4b−a24b - \dfrac{a}{2}

  5. a+ba + b

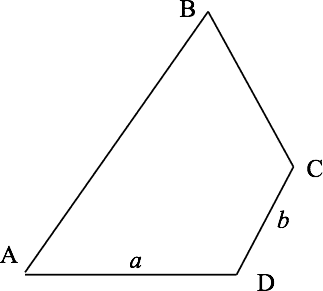
Solution

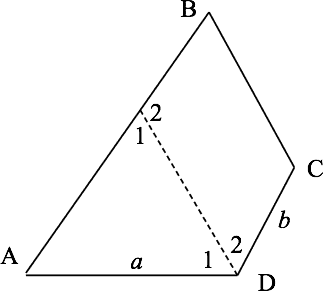
Draw DEDE to bisect ∠D\angle D. Then ∠D1=∠D2=∠B\angle D1 = \angle D2 = \angle B.

Now ∠B+∠C−180\angle B + \angle C - 180, so ∠D2+∠C=180\angle D2 + \angle C = 180 and ED∥BC ED \parallel BC. So BCDEBCDE is a parallelogram and EB=bEB = b. Next,

∠E1=∠B⇝∠E1=∠D1⇝△AED is isosceles⇝AE=a.\begin{aligned}\angle E1 = \angle B &\leadsto \angle E1 = \angle D1 \\&\leadsto \triangle AED \text{ is isosceles} \\&\leadsto AE = a.\end{aligned}

Finally, AB=AE+EB=a+bAB = AE + EB = a + b. The answer is e.