3160.11 – Triangle ABC is Isosceles

Given: Triangle $\triangle ABC$ is isosceles with $AB = AC$. Side $AC$ is extended to point $D$ in such a way that $C$ is between $A$ and $D$ (but not necessarily the midpoint). Then $E$ is found between $B$ and $C4 so that$EC = CD$. DE is now extended to intersect$AB$at$F$.

To Prove: angle $\angle AFE$ is thrice the angle at $D$.

Solution

Let angle $\angle D = x$. Then $\angle E1 = x$ and $\angle C1 = 2x$ (exterior angle theorem). Then $\angle B = 2x$ and $\angle F1 = 3x$ (exterior angle again).

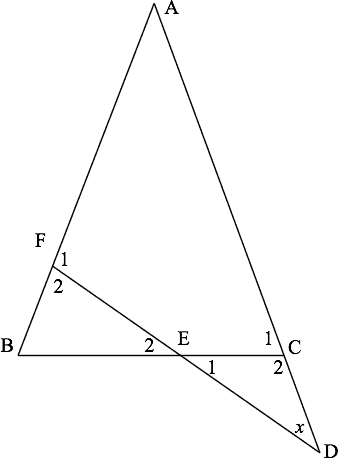
QED. (Which stands for "Quod Erat Demonstrandum", meaning "that which was to be proved.")