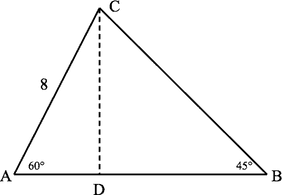
In triangle ABC (see figure), angle A is 60 degrees, angle B is 45 degrees, and the length of AC is 8. What are the lengths of the other two sides? You can bang out the answers using the Law of Sines, but with those nice angles surely there is another way.
Solution
With the altitude from C drawn, triangle CAD is a 30-60-90 triangle and triangle CDB is a 45-45-90 triangle. Hence AD = 4 and CD = 4. Since DB also is 4, we find that CB = 4 and AB = 4 + 4.
