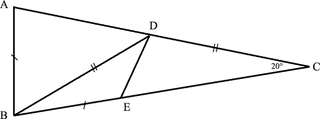
3155.41 – A Mystery Angle

In the figure, triangle ABC has CA = CB and angle C = 20 degrees. In addition, BD = DC and BE = BA. What is angle BDE?

Detailed Hint: Draw the arc of a circle with center B and radius BD meeting BA extended at X and BC at Y. Draw segments DX and DY.

Solution

The figure shows the arc and lines suggested by the hint. To find angle BDE = D3, we find D2, D4, and D5. Then subtract from 180 degrees.

Triangle ABC is isosceles, therefore A1 = 80 degrees. triangle BDC is isosceles, therefore B2 = 20 degrees and B1 = 60 degrees. Note also that A2 = 100 degrees.
Triangle BDY is isosceles, therefore Y1 = D3 + D4 = 80 degrees. So D5 = 60 degrees. Note that Y2 is now 100 degrees.
Triangle XBD is isosceles with B1 = 60 degrees, therefore triangle XBD is equilateral, hence angle X = 60 degrees and XD = BD = DC.
Angle X = D5, XD = BD = DC, and D1 = angle C = 20 degrees, therefore triangle XAD $\cong$ triangle DYC by ASA.
From 4, we get XA = DY.
Since BX - BA = BY - BE, XA = EY. Thus EY = DY and triangle DYE is isosceles.
We now conclude that E2 = D4 = 50 degrees.
In triangle BAD, D2 = 180 - B1 - A1 = 180 - 60 - 80 = 40.
D3 = 180 - D2 - D4 - D5 = 180 - 40 - 50 - 60 = 30 degrees.

This is the answer!