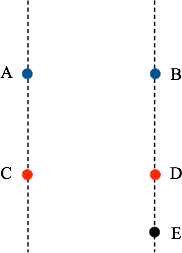
Suppose every point in a plane is colored either red or blue. Show that there are three points in the plane which are the same color and which determine a right angle.
Solution
If all of the points in the plane are red, then we're done. How many blue points would it take to make it impossible for there to be a red right angle? There must be at least two (and undoubtedly many more, but we just need two at the moment.) In the diagram, and are blue. Add points and so that lines and are parallel and are arranged as shown. Name a point somewhere on either line. No matter whether is red or blue we have our right angle.