2770.31 – Trisection Points

Two lines in the $xy$ -plane are drawn through the point $(3, 4)$ and the two trisection points of the line segment joining the points $(-4, 5)$ and $(5, -1)$ . Which of the following choices is the equation of one of these lines?

$3x - 2y - 1 = 0$
$4x - 5y + 8 = 0$
$5x + 2y - 23 = 0$
$x + 7y - 31 = 0$
$x - 4y + 13 = 0$

Solution

Between $A$ and $B$ , $\triangle x = 9$ and $\triangle y = 6$ . Consult the figure below.

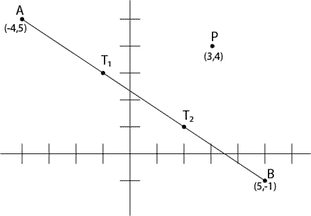
So, $T_1 = ( 4 + 3, 5 - 2) = (-1,3)$ , and $T_2 = (-4 + 6, 5 - 4) = (2, 1)$ . We find the slopes of $T_1 P$ and $T_2 P$ and see if they match the given equations’ slopes.

Slope $T_1 P$ : $m = \dfrac{4 - 3}{3 - 1} = \dfrac{1}{4}$ (e?)

Slope $T_2 P$ : $m = \dfrac{4 - 1}{3 - 2} = \dfrac{3}{1} = 3$ (nope)

So it seems to be (e).

Check: $x - 4y + 13 = 0$ Does it contain $T_1$ ? $-1 - 4(3) + 13 = 0$ . OK.

Does it have $P$ ? $3 - 4(4) + 13$ . OK.

The answer is, in fact, (e).