One sunny autumn morning, Barnabas was out for his usual stroll along a high railroad overpass, right next to the track, listening for bird calls. Many sounds caught his attention: sparrow chatter, the familiar piercing scree of a red-tailed hawk, and... a curious whisper in the distance? Some sort of mechanical ticking, a protracted scrape of metal on metal, a fog of white noise growing thicker with each second? A train behind him!
Barnabas ran ahead to the far end of the overpass and hopped off just as the train caught up with him. After the shock had dissipated and noting that he was of the way across the bridge when he heard the train, he wondered whether he could have run backward, toward the train that is, instead and still gotten off in time.
Analyze this. Under what circumstances could he have escaped the train by running either way?
Solution
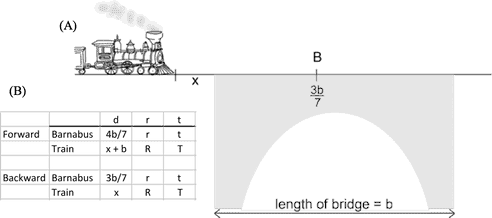
The figure, part (A), depicts the scenario. Part (B) begins the analysis with the usual table. Note that there are two rates (one for Barnabus and one for the train) and two times (one for motion forward and one for motion backward. There are also two distances for Barnabus (from the two ends of the overpass) and two distances for the train as well (also from each end of the overpass).
From the table we write two equations, one for each direction of travel. First, forward:
then backwards:
Subtracting, leads to .
So the train goes 7 times as fast as Barnabas. When he runs , the train goes , which tells us . If the train is 3 times the length of the bridge away (or more), then Barnabas can run in either direction and escape catastrophe.
Query: Can you generalize this? What if he's of the way across instead of ...?
And a final inconvenient question: How on earth did he know he was of the way across the bridge?