2440.71 – Uther and Eethyl

Uther can run at a constant speed of kk yards per second. Eethyl is faster: she can run xx times as fast as Uther, (so x>1x > 1).

Suppose Eethyl gives Uther a head start of yy yards, and then they both start running at the same time in the same direction. How many yards will Eethyl run before she catches up with Uther? Your answer will be some kind of a formula involving the variables in this problem.

Solution

Filling in the chart: Let dd be the distance Eethyl runs, so d−yd - y equal Uther's distance. Let rr be the rate of speed given for each person above in the problem.

The time tt is the same for each row by construction. (We are describing the singular moment Eethyl catches up to Uther.)

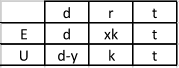
Observe that time=distancespeed\text{time} = \dfrac{\text{distance}}{\text{speed}}. So,

dxk=d−ykdk=xk(d−y)d=x(d−y)d=xd−xyxd−d=xyd(x−1)=xyd=xyx−1\begin{align*}\dfrac{d}{xk} &= \dfrac{d-y}{k} \\[1em]dk &= xk(d-y) \\[0.5em]d &= x(d - y) \\[0.5em]d &= xd - xy \\[0.5em]xd - d &= xy \\[0.5em]d(x-1) &= xy \\[0.5em]d &= \dfrac{xy}{x-1}\end{align*}