2440.63 – Rashon and Santiago

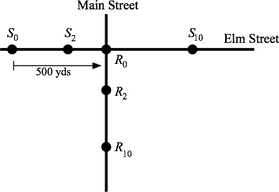
Rashon and Santiago walk at constant speeds along Main and Elm streets respectively. When Rashon is at the intersection – they are perpendicular streets – Santiago is still 500 yards away. Two minutes later, they are the same distance from the intersection. And in another eight minutes, they are again equidistant from the intersection. Got that?

OK! Suppose Rashon walks at rr yards per minute and Santiago at ss yards per minute. What is the ratio rs\dfrac{r}{s}?

Solution

Let RtR_t and StS_t be the positions of Rashon and Santiago along their respective streets at time tt, so that, for example, R2R_2 represents the position of Rashon along Main Street after two minutes. Note that we take Main Street to be vertical while Elm Street is horizontal. The figure below sketches the action. RR gives the vertical or yy coordinate; SS gives the horizontal or xx coordinate. In particular, note that R2R_2 and R10R_10 are negative.

In terms of rr and ss, the positions of RR and SS are given in this table:

tRS00−5002−2r2s−50010−10r10s−500\begin{array}{c|c|c}t & R & S \\\hline 0 & 0 & -500 \\2 & -2r & 2s - 500 \\10 & -10r & 10s - 500\end{array}

The relative locations of Rashon and Santiago after 2 and 10 minutes, then boil down to the two equations:

S2=R2S10=−R10.\begin{aligned}S_2 &= R_2 \\S_{10} &= -R_{10}.\end{aligned}

Using the table, this becomes the set of equations

2s−500=−2r10s−500=10r\begin{aligned}2s - 500 &= -2r \\10s - 500 &= 10r\end{aligned}

or

r+s=250r−s=50\begin{aligned}r + s &= 250 \\r - s &= 50\end{aligned}

It turns out that r=150r = 150 and s=100s = 100. Thus rs=32\dfrac{r}{s} = \dfrac{3}{2}.