2440.21 – Duckburg to Possumtown

Huey, Dewey, and Louie must get from their home in Duckburg to a friend's house in Possumtown, a distance of 52 km. Louie has a motorcycle that can go 20 kph but no faster and can only manage a single passenger. The three make a plan. Louie will take Huey part of the way and then leave him to waddle the rest (at 5 kph--very good speed for a duck). Then Louie will go back and pick up Dewey, who has been waddling along all this time (at 4 kph). The two of them will ride on to Possumtown. The plan works perfectly: all three arrive at their destination at the same time.

Tell me: how many hours did it take for them to get from Duckburg to Possumtown?

Solution

A chart for this problem is below. The three variables, $x, y, z$ , are times: $x$ is the time that Huey rides, $y$ is the time that Huey walks, and $z$ is the time that Louie takes to go back and pick up Dewey. Check that the distances in the chart are correct. Check that each duck travels for $x + y$ minutes so that this is the answer to the problem.

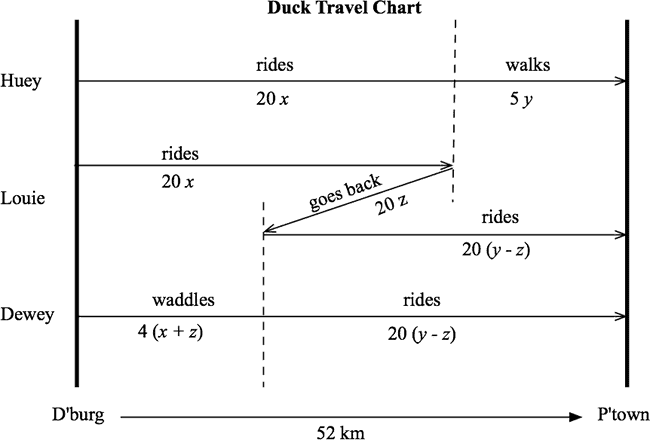
The algebraic sums of the distances each duck travels are:

\begin{aligned} H&:& \text{ } 20 x + 5 y &=& 20 x + 5 y \\ D&:& \text{ } 4(x + z) + 20(y - z) &=& 4x + 20 y -16z\\ L&:& \text{ } 20x - 20z + 20(y - z) &=& 20x + 20 y - 40 z. \end{aligned}

Each duck travels the same net distance of 52 km. This gives three equations in the three unknowns:

\begin{aligned} 20 x + 5 y + 0 z &=& 52 \\ 4x + 20 y -16z &=& 52 \\ 20x + 20 y - 40 z &=& 52. \end{aligned}

Solving this set of equations gives $x = 1.8, y = 3.2, z = 1.2$ . The answer is $x + y = 1.8 + 3.2 = 5$ hours!