Your science class is on a field trip to a rocket testing site. A rocket sled on a track passes the place where you are standing, traveling 900 meters per second (the sled, not you). Two hundred and seventy meters farther down the track it explodes unexpectedly. If you hear the sound of the explosion 1.1 seconds after the sled passes by, you can calculate the speed of sound. Do it.
Solution
Discussion: This is not particularly difficult, but it gives good practice in breaking a problem up into steps, as well as giving some practice with the formula.
Solving the Problem: A drawing is essential. See the one below.) The drawing helps us to see that the 1.1 seconds is timing two things: the time it takes the sled to reach the point of its demise, and the time it takes for the sound to come back. If we calculate the time it takes the sled to travel the 270 meters to its explosion point, the remaining time is what it takes the sound to travel 270 meters back.
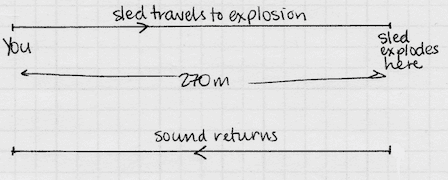
So, at 900 meters per second, it will take seconds to travel to its explosion point – that's 0.3 seconds. Subtracting, seconds for the sound to travel 270 meters back.
, so the calculated speed of sound is meters per second.
Heuristics: #5, draw a picture, and #13: break the problem up into steps (sub-goals).
Using the Problem with Students: I like this problem in an algebra class where the d = rt formula has been on stage. The impulse is to divide 270 by 1.1 and say the problem is done. The result of that division is 245.45, and I'll simply say that that's a wrong answer. Then the students need to start thinking a bit harder, to find out why.
Modifying/Extending the Problem: The speed of sound varies with altitude and temperature. Students might be asked to find out the circumstances under which the calculated answer of 337.5 is correct.
Remarks: I have given this problem in another version, in which it's stated that "you hear the sound 1.1 seconds after the sled passes you. Calculate the speed of sound." A problem stated this way can be extremely annoying to students, as it well should be: it's totally unrealistic. While one could go and measure the distance of 270 meters to the place where the sled exploded, it is inconceivable that anybody would have measured the 1.1 seconds.
Indeed, it's far more likely that whoever made up the problem would use the known speed of sound to calculate the time you'd hear the explosion, rather than the other way around. We owe our students the chance to air grievances about problems that are unrealistic. Once they've had their say, we can ask them to suspend their disbelief, a la Samuel Taylor Coleridge, to be charitable toward the poor folks who make up lame problems, and to accept the challenge of solving such problems anyway. After all, in the gym, we lift weights so that we can use our strength in "real" situations – and Stellas can be thought of as barbells for the brain.
An unrealistic problem can still give a good workout. However, all of that having been said, one tries to make problems realistic where possible, which is why I couched this one in terms of "if".