2260.41 – Two Cubes

Let $x$ and $y$ be the two side lengths. The combined volume is $x^3 + y^3$ while the combined lengths of all sides (12 per cube) is $12 x + 12 y$. Thus we are looking for a whole-number solution of the equation:

$$x^3 + y^3 = 12 x + 12 y$$

or

$$x^3 + y^3 - 12 x - 12 y = 0$$

Since only integer solutions are sought and the quantity $x^3 + y^3 - 12 x - 12 y$ grows larger and larger as $x$ and $y$ grow, any solution will be in a small region of the first quadrant. This is perfect for a computer search, using your spreadsheet. Tabulating $x^3 + y^3 - 12 x - 12 y$ for values of $x$ and $y$ between 1 and 6 gives the result shown in the figure.

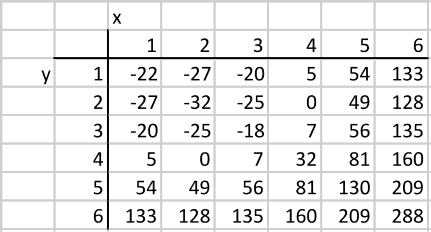
There is a solution $x = 4, y = 2$ (and with these values reversed). As the values at the edge of the table will only grow larger, this must be the only solution.