2240.11 – A Butterfly Garden

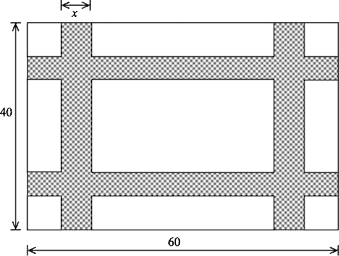
At a nearby retirement home, a large garden (for butterflies) is being planned. It will be 40' by 60', and will be crossed by four straight smooth paths, all the same width, as seen in the figure below. Turning this into a puzzle for you, if the total area of the paths is 736 square feet, how wide is each path?

Solution

If $x$ is the width of the paths (as in the figure below) then we can compute the area as follows:

$736 \text{ ft}^2 = 2 x \cdot 60 + 2x \cdot 40 - 4x^2$

Here the term $2x \cdot 60$ is the area of the two horizontal paths, $2x \cdot 40$ similarly is the area of the vertical paths, and because the square patches where the paths cross are now each counted twice we must subtract $4 x^2$ . From the equation above we derive the quadratic:

$0 = 4x^2 - 200x + 736 = 4 (x - 4) (x - 46).$

Discarding the irrelevant root $46$ , we find that $x = 4 \text{ ft.}$

This is certainly wide enough for one wheelchair, but perhaps not for two unless they take turns going, or unless one-way signs are posted.