Find all real solutions to the inequality .
Solution
Graph and . Below is such a graph from to . You see that disappears when and disappears for , when the two quantities stop being real.
As for ? That happens when .
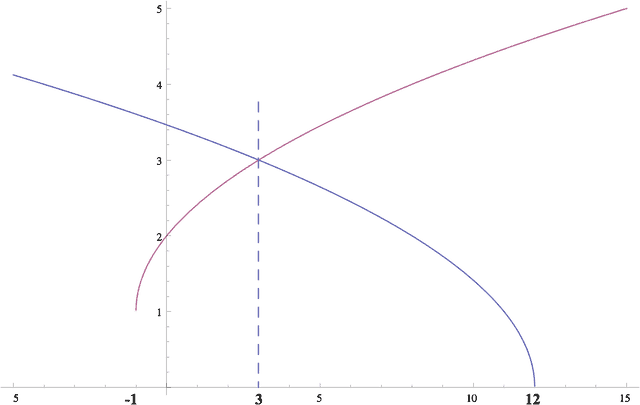
Find all real solutions to the inequality .
Graph and . Below is such a graph from to . You see that disappears when and disappears for , when the two quantities stop being real.
As for ? That happens when .
