2210.71 – Point on a Line. Making a Triangle?

Given points A, B, C, and D are distinct and lie, in that order, on a straight line. Line segments AB, AC, and AD have lengths $x$ , $y$ , and $z$ , respectively. Suppose that the line segments AB and CD are rotated about points B and C, respectively, so that points A and D coincide and thereby form a triangle with positive area (see the figure below), then which of the following three inequalities must be satisfied?

I: $x < z/2$

II: $y < x + z/2$

III: $y < z/2.$

Solution

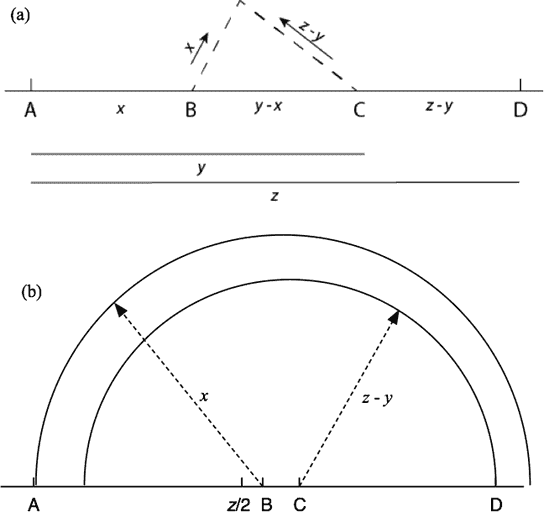
In summary, I and II are true.

In the first place, II must be satisfied. Consider this chain of reasoning, based on the figure above, part (a):

$\begin{aligned}x + z - y &> y - x \\2 x + z - 2 y &> 0 \\2 x + z &> 2 y \\x + \dfrac{z}{2} &> y\end{aligned}$

So statement II must be satisfied. It happens that inequality I is also true. The figure, part (b), explains why informally. Can you prove it?

Finally, the figure, part (a), shows that III may be violated.