2210.41 – Distance on the Number Line

The locus of points $P$ on the number line such that the distance between $P$ and the point $2$ is between $1$ and $7$ is

$x \leq 1$ or $x \geq 3$
$1 \leq x \leq 3$
$-5 \leq x \leq 9$
$-5 \leq x \leq 1,$ or $3 \leq x \leq 9$
$-6 \leq x \leq 1$ or $3 \leq x \leq 10$

Solution

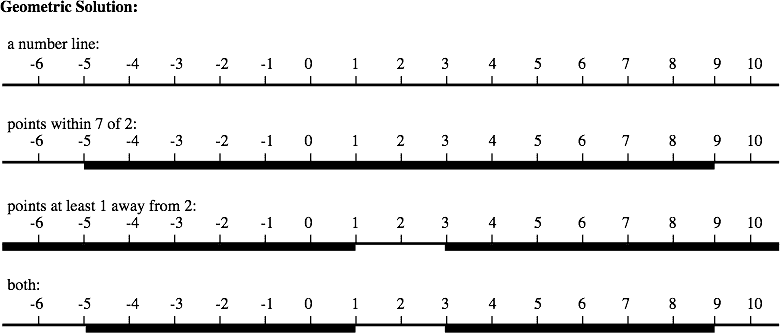
The answer is (d). Find it by drawing it! The figure far below shows how.

Or use algebra. The distance between points $x$ and $y$ on a line is $|x - y|$ , so the given condition on $P$ is that $1\leq |P - 2|\leq 7$ . Let's take the two parts of this separately and see what they mean.

In the first place, $1\leq |P - 2|$ means either $1 \leq P - 2$ or $P - 2 \leq -1.$ In other words, either $3\leq P$ or $P\leq 1.$ On the other hand, $|P - 2|\leq 7$ means that $-7 \leq P - 2\leqq 7,$ and this means $-5 \leq P\leq 9.$ Putting these together (which probably means drawing the picture), we see that either $3\leq P\leq 9$ or $-5\leq P\leq -3.$ This is (d).