2210.21 – Inequality

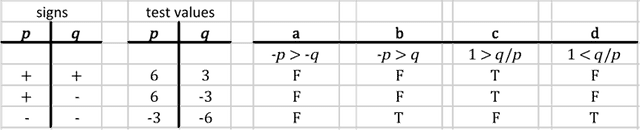
Suppose $r > 0$ . Then which of the alternatives below is true for all $p$ and $q$ such that $pq \neq 0$ and $pr > qr$ ?

$-p > -q$
$-p > q$
$1 > q/p$
$1 < q/p$
none of these

Solution

Since $r$ is not equal to 0, we can divide by $r$ , and since $r$ > 0 we know $pr > qr$ implies $p > q$ . This makes $p < 0$ and $q > 0$ impossible. In the table below the three remaining possible signs for $p$ and $q$ are tested.

Since none of the conditions (a), (b), (c), or (d) holds for every possibility of $p$ and $q$ , (e) is correct.