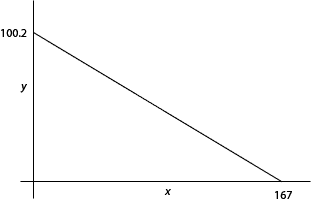
The number of positive integer solution pairs of the equation is:
33
34
35
100
none of these.
Solution
The graph is below. The question is: through how many lattice points does the straight line pass?
We could simply tabulate the values of for all integral using a spreadsheet and count the number of integer values.
Or, if we use a calculator, we soon see that is an integer when and so on. This suggests that there are two usable values of in every interval , except in the last one where 167 is not usable. There are 16 such intervals, each with two good 's, plus the extra: . That makes good 's, or 33 lattice points. The answer is (a).