2162.11 – An Infinite Continued Fraction

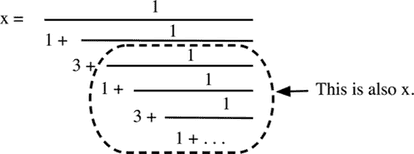
The fraction in the figure below keeps going forever following the pattern. What is its value? (Hint: You will need the quadratic formula.)

Tags:
Solution

The key to this problem is to notice that this fraction contains a copy of itself, as indicated in the figure. Therefore,

x=11+13+x=13+x+13+x=3+x4+x x = \dfrac{1}{1+\dfrac{1}{3+x}} = \dfrac{1}{\dfrac{3+x+1}{3+x}} = \dfrac{3+x}{4+x}

Cross-multiplying and gathering terms give the quadratic equation:

x2+3x−3=0 x^2 + 3x -3=0

whose solutions are x=−3±212x = \dfrac{-3 ± \sqrt{21}}{2}. As xx is clearly positive, we go with the plus sign, and find that x=−3+212≈0.79x = \dfrac{-3 + \sqrt{21}}{2} \approx 0.79.