The marks on the faces of these gears are aligned as shown.
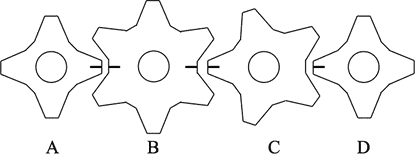
What is the least number of turns that gear must make so that the marks are all re-aligned in their original position? (Note: Gear has two options for "original". Either one is OK.)
Solution
Let's define "turn" as a complete turn, and let's define "click" as a partial turn of one notch on a wheel.
will return to its original position after any multiple of four clicks.
will return to its original position after any multiple of three clicks (see the note in the statement of the problem).
will return to its original position after any multiple of five clicks.
will return to its original position after any multiple of four clicks (same as ).
The least common multiple of these click numbers is 60. If makes 60 clicks it will be in its original position after 15 turns. will be in its "original" position after 20 turns. will be in its original position after 12 turns. And will be in its original position after 15 turns.
So we see that if makes 15 turns everything will be fine.