2100.32 – Sums of Odd Numbers

Look at the figure:

  1. What does A have to do with B?

  2. Continue both A and B for two more "parts".

  3. Find the totals in A. What kind of numbers are they?

  4. Does B tell you why these numbers are what they are? Explain.

  5. What is 1 + 3 + 5 + 7 + . . . + 99?

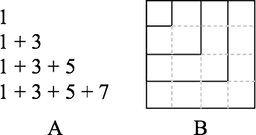
Solution

  1. You can find each number in the picture.

  2. 1 + 3 + 5 + 7 + 9; 1 + 3 + 5 + 7 + 9 + 11

  3. 1, 4, 9, 16, 25, 36: perfect squares.

  4. You can see the squares!

  5. Let's work up to it:

    1+3=4=221+3+5=9=32=(1+52)21+3+5+7=16=42=(1+72)2\begin{aligned}1 + 3 = 4 &= 2^2 \\1 + 3 + 5 = 9 &= 3^2 = (\dfrac{1+5}{2})^2 \\1 + 3 + 5 + 7 = 16 &= 4^2 = (\dfrac{1+7}{2})^2\end{aligned}
    So 1+3+5+7+…+99=(1+992)2=502=2500\text{So } 1 + 3 + 5 + 7 + \ldots + 99 = (\dfrac{1+99}{2})^2 = 50^2 = 2500