2070.33 – A Rectangular Box

A rectangular box without a top is formed by cutting squares from the corners of an 8×158 \times 15 sheet of cardboard and then folding up the sides. Let xx be the side of the square cutouts. Then determine the following:

  1. a formula in terms of xx that gives the volume of this box

  2. whether this a quadratic formula

  3. the domain of xx-values relevant to this problem

Solution

According to the diagram below, the dimensions of the box are 15−2x×8−2x×x15-2x \times 8 - 2x \times x.

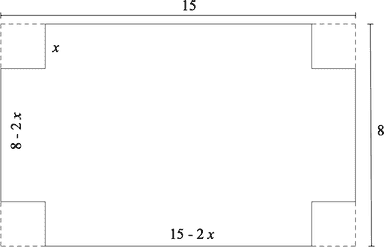
  1. The volume is V=x(8−2x)(15−2x)=120x−46x2+4x3V = x (8 - 2x)(15-2x) = 120x - 46 x^2 + 4 x^3.

  2. This is a cubic rather than a quadratic.

  3. The relevant values of xx are 0<x<40 < x < 4. If xx is outside these limits then the box disappears, that is, it has a length negative or zero in some direction.

Note: A standard calculus problem is to find the value of xx that maximizes the volume of the box. Calculus is good for finding maximums or minimums of things. You could also set the problem up on a spreadsheet to hone in on the answer.