1720.11 – TTT

A good way to start is by considering $E$ because both $YE$ and $ME$ end with it. Whatever the value of $E$, its square determines the last digit of the product, $TTT$, and hence the whole product.

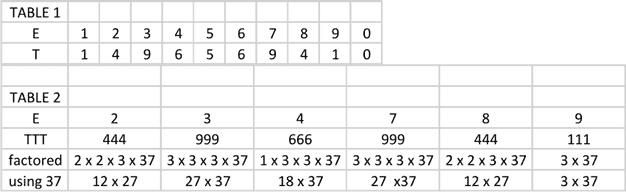
TABLE 1 below lists all of possible values for $E$ together with the value of $T$ implied. We can rule out the values that make $T = E$ because the letters stand for unique digits. Thus we eliminate $E = 1, 6, \text{ or } 0$.

TABLE 2 lists the remaining possibilities for $E$, together with the whole resulting number $TTT$ and its prime factorization. From the table we see clearly that, when writing $TTT$ as a product of two two-digit numbers, one of those numbers must be $37$.

Because one of our two numbers must be $37$, we know that the other must end in 7 as well. Examining the table, we find that only $E = 7$ works. We now know that:

We were really asked for the sum $E+M+T+Y=7+3+9+2=21.$ That turns out to be 21. The answer is c.